虚数的模具体是什么意思？虚数模的计算方法是什么？

数学领域中的复数一直是理解抽象概念的重要部分，而虚数的模则是复数理论中的一个核心概念。对于初学者来说，虚数的模可能看起来有些抽象，但实际上它是描述复数与实数轴距离的一种方式。理解虚数的模，不仅有助于深入学习数学，还可以在物理学、工程学及其他科学领域中找到广泛的应用。

一、复数与虚数的模基础概念

复数是由实数部分和虚数部分组成的数，可以表示为a+bi的形式，其中a和b是实数，i是虚数单位，满足i2=-1。复数的模（或绝对值）是复数在复平面上到原点距离的度量。对于复数a+bi，其模定义为√(a2+b2)。

1.1什么是虚数？

在数学中，虚数是不能用实数表示的数，它们是实数的扩展。虚数的核心在于虚数单位i，根据定义，i2=-1。2i是一个虚数，因为它只能用虚数单位和实数的乘积来表示。

1.2复数的表示

复数不仅可以表示为a+bi的形式，也可以在复平面上表示为一个点或向量。该平面被称作复平面或阿尔冈图，横轴为实轴，纵轴为虚轴。

二、虚数的模具体是什么意思

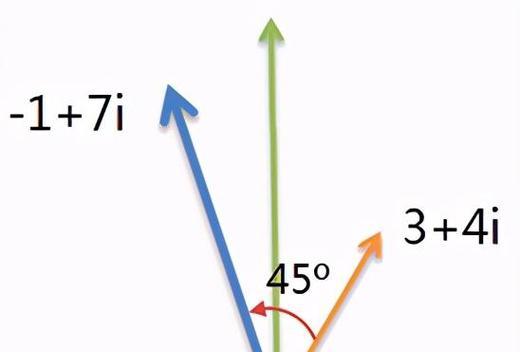
虚数的模实际上描述的是复数在复平面上的位置与原点之间的欧几里得距离。这意味着，如果我们把复数想象成复平面上的一个点，那么这个点到原点的直线距离就是其模。

2.1模的数学定义

对于复数z=a+bi，其模|z|定义为：

\[|z|=\sqrt{a^2+b^2}\]

这里a是复数的实部，b是复数的虚部。

2.2模的几何意义

几何上，模是复数点到复平面原点的距离。你可以使用直角三角形的勾股定理来直观理解它，其中实部和虚部分别作为三角形的两个直角边，模就是斜边。

三、虚数模的计算方法

计算虚数的模并不复杂，遵循基本的数学运算规则即可完成。

3.1直接使用定义公式

对于任何非零复数z=a+bi，你只需要按照下列步骤计算模：

1.确定实部a和虚部b的值。

2.将实部和虚部的值平方。

3.将两者相加得到一个和。

4.取该和的平方根。

模就是：

\[|z|=\sqrt{a^2+b^2}\]

3.2示例计算

假设我们要计算复数z=3+4i的模，步骤如下：

1.实部a=3，虚部b=4。

2.平方得a2=9，b2=16。

3.相加和为9+16=25。

4.最后取平方根√25=5。

复数3+4i的模是5。

3.3注意事项

如果复数为纯虚数，即形式为0+bi，其模为|b|。

如果复数为实数，即形式为a+0i，其模为|a|。

零的模是零，即|0|=0。

四、虚数模的应用

虚数的模不仅在纯数学领域有其重要性，也广泛应用于工程、物理和信号处理等实际问题中。

4.1工程学

在电子工程中，交流电的幅值常通过计算其复数表示形式的模来确定。

4.2物理学

量子力学中，波函数的模的平方可以解释为粒子在某位置出现的概率密度。

4.3信号处理

在信号处理领域，信号的频率响应可以通过复数表示，其模可作为信号幅度的度量。

五、虚数模计算中的常见错误和问题

在计算虚数的模时，初学者可能会遇到一些常见问题，理解下面这些要点有助于避免这些错误：

5.1模总是非负数

由于模是距离的概念，因此它永远是正数或零。

5.2复数为零时模的特殊性

特别需要注意的是，复数为零时，即z=0+0i，其模为零。

5.3模的乘法性质

如果复数z1和z2，那么|z1*z2|=|z1|*|z2|。即两个复数模的乘积等于它们相乘后模的值。

六、

理解虚数的模是深入复数理论及其它数学分支的关键步骤。虚数的模为我们提供了一种衡量复数在复平面上相对位置的量化方式。通过掌握虚数模的计算方法，无论是在学习数学，还是在应用数学解决实际问题时，都将更加得心应手。希望本文的介绍已经为您清晰地解释了虚数模的概念及其计算步骤，并且通过相关应用的介绍，为您展示了这一数学概念在现实世界中的重要性。