直线对称的性质（探究直线对称及其应用）

它描述了一个图形关于某条直线对称、直线对称是几何学中一个重要的概念。我们将深入探讨直线对称的性质及其应用，在这篇文章中，帮助读者更好地理解和应用这一概念。

直线对称的定义与特征

直线对称是指一个图形在某条直线上的两侧完全相同。并且连线垂直于对称轴，它们之间的距离相等，图形的每个点关于这条直线有一个与之对应的点。对称性和传递性等基本性质，直线对称也满足自反性。

直线对称与轴对称的区别与联系

而轴对称是基于一条轴进行的，但直线对称是基于一条直线进行的、直线对称与轴对称都是图形的基本变换方式。而直线对称图形则需要通过在对称轴上折叠才能完全重合，轴对称图形可以通过沿轴进行翻转得到自身。

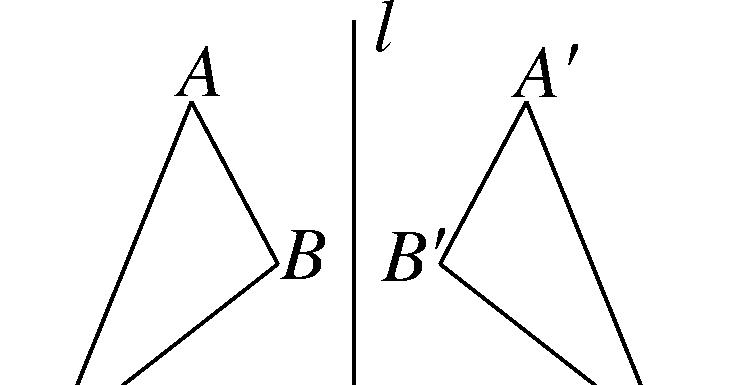
直线对称的基本应用

直线对称的基本应用包括图形的重叠与构造。或者判断两个图形是否关于某条直线对称，通过利用直线对称的性质，我们可以轻松地构造出与给定图形关于直线对称的图形。

直线对称与平面镜像的联系

直线对称可以看作是平面镜像在二维平面上的具体表现。在镜子中的图像与原图关于镜面对称、平面镜像也是图形的重要变换方式之一。即镜子是一条无厚度的直线，直线对称是平面镜像在二维平面上的特例。

直线对称与数学中的应用

直线对称在数学中有广泛的应用。可以通过直线对称判断一个函数是否是偶函数或奇函数，在代数学中；可以利用直线对称性质简化运算、在复数领域。

直线对称在物理学中的应用

尤其在电磁学和光学领域、直线对称在物理学中也有重要应用。反射光与入射光分布关于入射面对称，光的反射现象可以通过直线对称来解释。

直线对称在生物学中的应用

生物学中的很多结构都表现出直线对称的性质。这种对称性有助于生物体的生存和适应环境，人类的面部特征，动物的身体结构以及植物的花瓣等都具有直线对称性。

直线对称与艺术的关系

直线对称在艺术中也有广泛的应用。创造出美感和和谐感，许多艺术作品都运用了直线对称的原理。绘画中的镜像画法等都离不开直线对称的影响，建筑设计中的对称结构。

直线对称在日常生活中的应用

直线对称在我们的日常生活中也有很多应用。纸飞机等、如纸鹤，我们可以通过折纸来制作各种直线对称的手工艺品。家具和建筑设计等领域，直线对称也被广泛应用于衣物。

直线对称与对称加工技术

直线对称在制造业中的应用越来越广泛。减少制造过程中的浪费和成本、对称加工技术可以通过直线对称来提高产品的精度和质量。

直线对称的数学证明

直线对称的性质可以通过数学证明来加以验证。可以证明图形关于某条直线对称的几何性质，通过引入坐标系和向量运算等数学工具。

直线对称在几何证明中的应用

特别是在解决关于图形的对称性质、相似性和共线性等问题时，直线对称在几何证明中经常被应用。可以简化证明过程，提高证明的效率、通过利用直线对称的性质。

直线对称与现代科技的发展

直线对称在现代科技中发挥着重要作用，随着计算机技术和图像处理技术的发展。图像处理软件可以通过直线对称算法实现图像的自动修复和重建。

直线对称的发展与研究趋势

其研究和应用将会继续深入发展、直线对称作为一个基础概念。直线对称的性质和应用将会有更广阔的拓展和创新、随着数学和科学技术的不断进步。

它描述了一个图形关于某条直线对称，直线对称是几何学中一个重要的概念。应用及与其他领域的联系进行了详细的介绍和探讨、特征、本文通过对直线对称的定义。我们可以更好地理解和应用几何学中的相关知识，并在实际生活和科技领域中获得更多的应用，通过学习直线对称。